Kommognition
Hvordan forklarer børn tænkning?
Også yngre børn kan fortælle om, hvad tænkning er, og hvordan man kan forestille sig og forstå verden.

Her forklarer et barn, hvordan det kan være, at man kan forestille sig ting, der ikke findes.

Børn forklarer, hvad der sker i hjernen, når man tænker - og giver et bud på, hvordan drømme kan opstå.
Tænkning handler altid om noget. Det kan handle om en hændelse, en ting, et minde eller som her matematik. Neurologen Antonio Damasio skriver, at tænkning er ”indre tale”, der eksisterer som auditive eller visuelle billeder i vores bevidsthed. Hvis den indre tale ikke bliver til om end aldrig så flygtige billeder, ville den ikke blive til noget, vi kunne vide.
Samtidig kan tænkning forstås som en mental handling, altså en aktiv proces, der er tæt knyttet til sprog. Den russiske psykolog Lev Vygotsky spidsformulerer dette allerede i 1930'erne. Han skriver, at ”tænkning forløber i sproget”. Derfor er det en forudsætning for elevernes tænkning, at de får mulighed for at være sprogligt aktive.
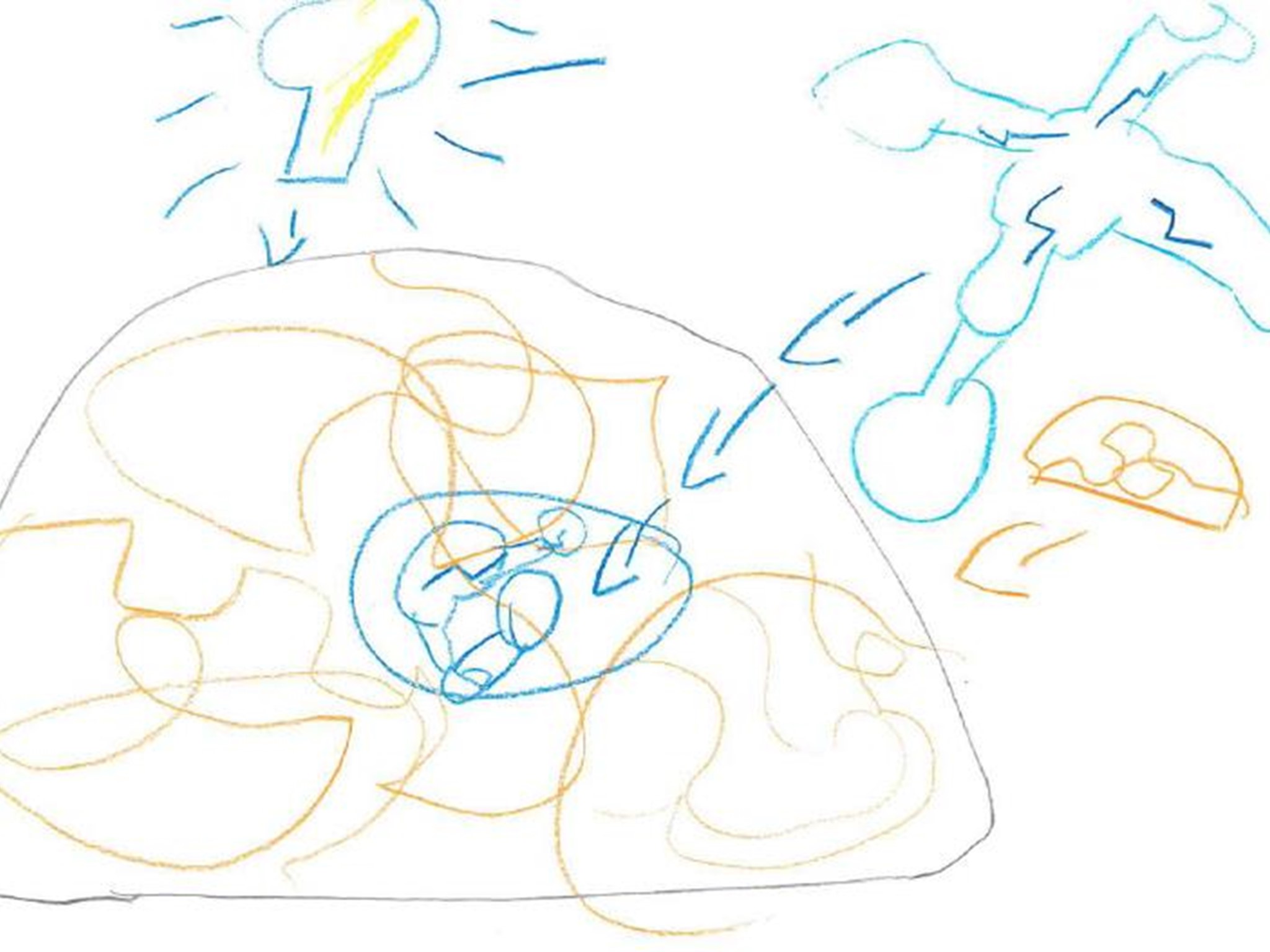
Barn i børnehaveklassen tegner og forklarer: "Det der sker inde i hjernen er blå tingester, der tænker. De arbejder virkelig hårdt. Når man gerne vil noget, har hjernen tænkt på det".
Den norske matematikdidaktiker Marit Høines skriver, at elevernes forståelser kan spejles i deres tegninger. Tegningerne afslører et budskab, og bliver på den måde et middel til tænkning og derfor en måde at kommunikere en indre dialog på.
Tegninger kan altså forstås som det konkrete udtryk for elevers forståelse. Gennem samtalen om en tegning kan læreren få indblik i elevens indre billeder og tænkning. Både lærer og elev kan bruge den forståelse, der er repræsenteret i tegningen, som udgangspunkt for at problematisere og tænke videre.
Et barn tegner og forklarer: "Jeg kan tænke på noget. Så får jeg en god ide, og så tegner jeg det".

Følgende er et eksempel på en samtale om en tegning af et gangestykke, hvor elevens forståelse udvikler sig i samtalen.
Når man kommunikerer om noget, skaber man mening sammen. I dialogen nedenfor er både lærers og elevs bidrag vigtigt. Læreren taler ikke til eleven, men med eleven. Hun udfordrer elevens tænkning ved at stille spørgsmål, der får eleven til selv at tænke videre - det er kommognition.
-
Klik og kik
 Luk
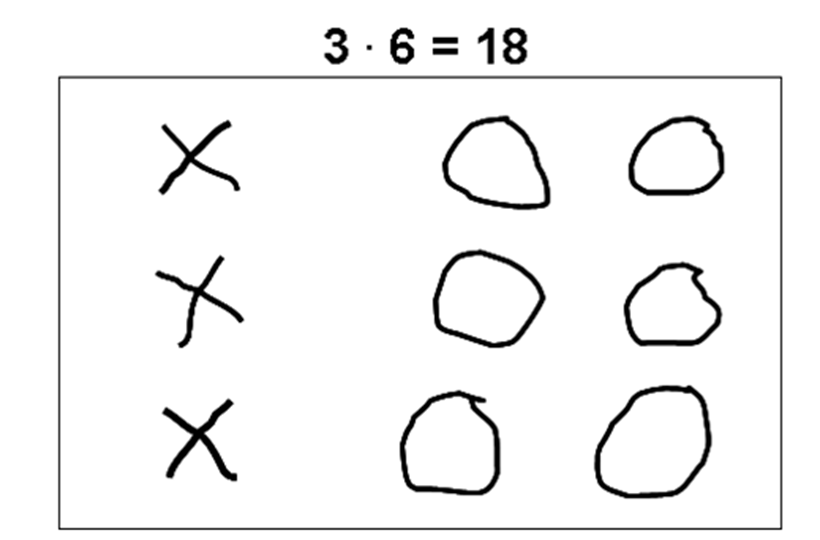
LukHvor mange i alt - af hvad?
Samtale mellem lærer (L) og elev (E). E: - Jeg har taget 3 krydser og ganget med 6 boller. L: Ja, og … E: Det bli´r 18 …. L: 18 hvad for noget? E: ja, 18 af... Jeg kommer igen lige om lidt!!
-
Klik og kik
 Luk
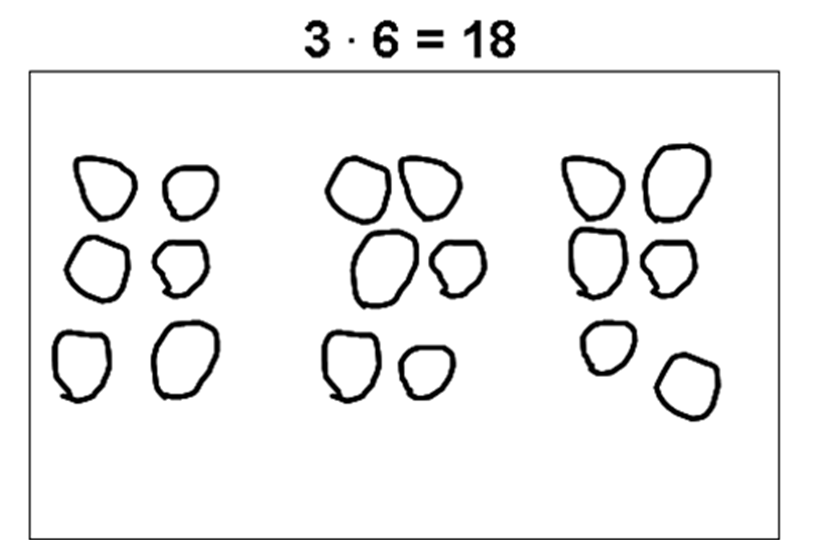
LukHvor mange i alt?
Anden samtale mellem lærer og elev. E: Nå, se nu. Nu er der 3 gange 6. L: Ja. Hvad mener du? E: Der er 3 gange 6 boller. Der er 18 boller i alt. Sådan!
-
Hvordan understøtter man elevers tænkning?
Klik og kik
LukGode spørgsmål sætter eleven på sporet:
Stil spørgsmål til elevens arbejdsproces, ikke kun til resultatet. Inddrag elevens tegninger eller andre repræsentationer. Giv eleven tid til at tænke, og byg videre på hendes input til samtalen.
Når man deltager i at løse et matematisk problem, skal der gerne være mulighed for kommognition.
Ind i den matematiske fortælling
Lad os se på et eksempel: Læreren lægger to små bunker slik på bordet og beder to elever om at finde ud af, hvor mange stykker slik der er i alt.
Ved at involvere sig i den matematiske diskurs "at finde ud af, hvor mange der er i alt", som fx inkluderer den matematiske rutine, hvor eleverne først tæller den ene bunke og derefter tæller videre i den anden bunke, mens de peger på hvert stykke slik, opbygger eleverne efterhånden en underbygget matematisk fortælling om, hvordan man finder ud af, hvor mange der er i alt.
Hvis elever deltager i tilstrækkelig mange “hvor mange er der i alt”-situationer, skifter tælleritualet til at blive en rutine for det enkelte barn, siger Anna Sfard. Barnets tænkning bliver herefter en individualiseret, mental udgave af den tidligere kommunikation med læreren eller den anden elev.
-
Klik og kik
 Luk
Luk
-
Klik og kik
 Luk
Luk
-
Klik og kik
 Luk
Luk
Tænkning skal synliggøres
Det er umiddelbart nemt at tale om noget konkret; så er det tydeligt, hvad man taler sammen om. En illustration af det, der samtales om, kan konkretisere og derfor understøtte og udvikle samtalen. Når vi bruger illustrationer og sætter ord på dem i samtaler, gør vi derved objekter og begivenheder til noget, vi kan tænke om.
Men hvad skal vi lytte efter i faglige samtaler med elever?
Sfard foreslår tre temaer, vi kan lægge mærke til i samtaler med elever
Hvilke matematiske fagord og begreber anvender eleverne i faglige sammenhænge - og hvordan anvender de dem?
Hvilke narrativer, det vil sige de sproglige sammenhænge, fagordene indgår i, producerer eleverne?
En elev siger for eksempel: “ Når man måler noget, finder man ud af, hvor lang en ting er”.
Hvilke strategier, eller rutiner, anvender eleverne i det faglige arbejde? Strategier er veldefinerede, gentagne mønstre eller mangel på samme, der er karakteristiske for den matematiske diskurs.
En elev lægger for eksempel linealen ved nul, når han måler.

To børn taler sig frem til forståelse
Et andet eksempel på parallelle opgaver
-
Mulighed 1
Klik og kik
LukVælg et tal mellem 2 og10. Vis tallet på så mange forskellige måder, du kan.
-
Mulighed 2
Klik og kik
LukVælg et tal mellem 20 og 30. Vis tallet på så mange forskellige måder, du kan.
Fra resultatorienterede til procesorienterede spørgsmål
Her kan du se et eksempel på, hvordan man kan hjælpe elever til at reflektere over matematik. Det handler om at stille åbne opgaver. Om at gå fra "hvor mange...?" til "Hvordan kan vi vide...?".
Mere om at stille opgaver
Spørgsmål, der kan indlede eller forlænge en samtale om matematik
- Prøv at forklare, hvorfor du tror det?
- Hvordan er du kommet til det resultat?
- Overbevis resten af os om, at det stemmer?
- Er der andre, der har samme svar, men en anden forklaring?
- Hvilke ligheder er der på jeres forklaringer?
- Hvilke forskelle er der på jeres forklaringer?
- Hvordan kan man vide, at det er sandt i alle sammenhænge?
- Hvad ved du? Hvad tror du?
- Hvordan kan man vise det ved hjælp af en model/illustration?
Spørgsmål, der kan støtte eleverne i at formulere og løse problemer
- Hvad tror du er problemet?
- Hvad mangler du for at kunne løse problemet?
- Hvilke oplysninger mener du er overflødige?
- Hvilke forslag kunne man forestille sig?
- Prøv med et gæt!
- Hvordan kan man formulere problemet på en anden måde?
- Hvad nu hvis …?
- Hvordan kan man ændre på problemet for at få andre løsninger?
- Hvilke sammenhænge kan du finde?
- Hvad har du arbejdet med før, der ligner dette problem?